Materi matematika ruang sampel merupakan fondasi penting dalam mempelajari peluang dan statistik. Dengan memahami konsep ruang sampel, kita dapat menganalisis kemungkinan hasil dari suatu percobaan. Topik ini akan menguraikan definisi, jenis-jenis, dan contoh penerapan ruang sampel, serta cara mempelajarinya secara efektif. Mari kita mulai perjalanan memahami ruang sampel.
Ruang sampel mencakup semua kemungkinan hasil dari suatu percobaan atau peristiwa. Setiap hasil individu disebut titik sampel. Dalam materi ini, kita akan mempelajari berbagai jenis ruang sampel, mulai dari yang diskrit hingga kontinu, serta bagaimana menentukan ukuran ruang sampel untuk setiap jenis. Kita juga akan membahas contoh-contoh soal dan penyelesaiannya, serta hubungannya dengan materi matematika lainnya.
Definisi Materi Matematika Ruang Sampel
Ruang sampel dalam matematika adalah himpunan semua kemungkinan hasil dari suatu percobaan atau eksperimen. Konsep ini fundamental dalam teori probabilitas, karena membantu dalam memahami dan menghitung peluang terjadinya suatu kejadian tertentu.
Definisi Singkat Ruang Sampel
Ruang sampel adalah himpunan semua hasil yang mungkin terjadi pada suatu percobaan. Setiap hasil dalam ruang sampel disebut titik sampel. Ruang sampel sering dilambangkan dengan S.
Konsep Dasar Ruang Sampel
Konsep dasar ruang sampel adalah mengidentifikasi semua kemungkinan hasil yang bisa terjadi dari suatu percobaan. Percobaan tersebut bisa berupa hal sederhana seperti melempar koin atau hal yang lebih kompleks seperti percobaan ilmiah. Mengenali semua kemungkinan hasil ini sangat penting untuk memahami probabilitas terjadinya suatu kejadian tertentu.
Contoh-contoh Sederhana Ruang Sampel
- Pelemparan koin sekali: Ruang sampelnya adalah Angka, Gambar. Ukurannya adalah 2.
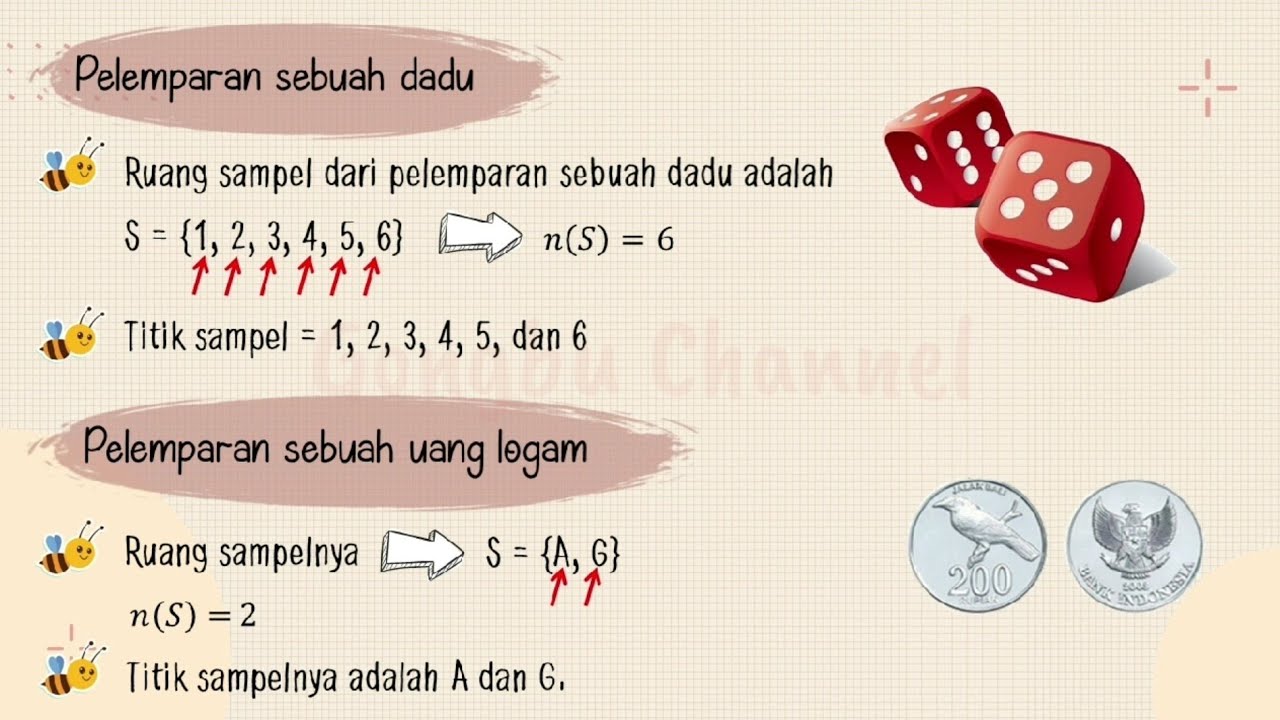
- Pelemparan dadu sekali: Ruang sampelnya adalah 1, 2, 3, 4, 5, 6. Ukurannya adalah 6.
- Pengambilan satu kartu dari seperangkat kartu bridge: Ruang sampelnya terdiri dari 52 kartu. Ukurannya adalah 52.
- Memilih warna bola dari kotak yang berisi bola merah, biru, dan kuning: Ruang sampelnya adalah Merah, Biru, Kuning. Ukurannya adalah 3.
Perbandingan Beberapa Contoh Ruang Sampel
| Contoh Percobaan | Ruang Sampel (S) | Ukuran Ruang Sampel (n(S)) |
|---|---|---|
| Pelemparan koin sekali | Angka, Gambar | 2 |
| Pelemparan dadu sekali | 1, 2, 3, 4, 5, 6 | 6 |
| Pengambilan satu kartu dari seperangkat kartu bridge | Himpunan 52 kartu | 52 |
| Memilih warna bola dari kotak yang berisi bola merah, biru, dan kuning | Merah, Biru, Kuning | 3 |
Perbedaan Antara Ruang Sampel dan Kejadian
Ruang sampel mencakup semua kemungkinan hasil yang mungkin terjadi dalam suatu percobaan. Kejadian adalah himpunan bagian dari ruang sampel. Artinya, kejadian adalah kumpulan beberapa titik sampel. Contohnya, kejadian “munculnya angka genap” pada pelemparan dadu adalah himpunan 2, 4, 6. Kejadian ini merupakan bagian dari ruang sampel 1, 2, 3, 4, 5, 6.
Jenis-jenis Ruang Sampel
Ruang sampel merupakan himpunan dari semua kemungkinan hasil suatu percobaan. Jenis-jenis ruang sampel dapat diklasifikasikan berdasarkan sifat datanya, yaitu diskrit atau kontinu. Pemahaman tentang jenis-jenis ruang sampel ini penting dalam menganalisis dan menginterpretasikan hasil percobaan.
Ruang Sampel Diskrit
Ruang sampel diskrit terdiri dari sejumlah berhingga atau tak terhingga yang dapat dihitung dari hasil percobaan. Data dalam ruang sampel diskrit biasanya berupa bilangan bulat atau kategori yang dapat dihitung. Contohnya, hasil lemparan koin, hasil pelemparan dadu, atau jumlah mobil yang lewat di jalan dalam satu jam.
- Definisi: Ruang sampel diskrit merupakan himpunan yang beranggotakan hasil percobaan yang berhingga atau dapat dihitung.
- Contoh: Pelemparan sebuah koin (S = Angka, Gambar), pelemparan sebuah dadu (S = 1, 2, 3, 4, 5, 6), atau jumlah pelanggan yang mengunjungi toko dalam sehari.
- Cara menentukan ukuran ruang sampel: Menentukan jumlah elemen dalam himpunan ruang sampel. Misalnya, dalam pelemparan koin, ukuran ruang sampel adalah 2 (Angka dan Gambar).
Ruang Sampel Kontinu
Ruang sampel kontinu terdiri dari hasil percobaan yang bernilai dalam suatu interval tertentu. Data dalam ruang sampel kontinu dapat mengambil nilai pada rentang nilai yang tak terhingga. Contohnya, tinggi badan, berat badan, atau suhu ruangan.
- Definisi: Ruang sampel kontinu merupakan himpunan yang beranggotakan hasil percobaan yang nilainya dapat mengambil nilai dalam suatu interval.
- Contoh: Tinggi badan siswa dalam suatu kelas, berat badan produk yang diproduksi, atau suhu udara di suatu kota dalam satu minggu.
- Cara menentukan ukuran ruang sampel: Menentukan panjang interval atau rentang nilai dalam ruang sampel. Misalnya, tinggi badan siswa dalam rentang 150 cm hingga 180 cm.
Perbedaan Karakteristik
| Karakteristik | Ruang Sampel Diskrit | Ruang Sampel Kontinu |
|---|---|---|
| Jenis Data | Bilangan bulat atau kategori yang dapat dihitung | Bilangan riil dalam suatu interval |
| Jumlah Hasil | Berhingga atau dapat dihitung | Tak terhingga |
| Representasi | Himpunan terurut atau terdaftar | Interval atau rentang nilai |
| Ukuran | Bilangan bulat | Bilangan riil (panjang interval) |
Contoh Soal Cerita
Sebuah perusahaan memproduksi baut dengan panjang yang diharapkan 5 cm. Toleransi panjang baut adalah ±0,1 cm. Tentukan ruang sampel panjang baut yang diproduksi.
Penyelesaian: Panjang baut yang diproduksi berada dalam interval 4,9 cm hingga 5,1 cm. Ruang sampelnya adalah himpunan semua panjang baut dalam interval tersebut, yaitu [4,9, 5,1].
Contoh Soal dan Penyelesaian

Berikut beberapa contoh soal dan penyelesaian mengenai ruang sampel, dilengkapi dengan penjelasan langkah-langkahnya. Contoh-contoh ini akan membantu memahami konsep ruang sampel dan penerapannya dalam berbagai situasi.
Contoh Soal 1: Pelemparan Dua Koin
Seorang anak melempar dua buah koin secara bersamaan. Tentukan ruang sampel dari percobaan tersebut.
- Langkah 1: Identifikasi kemungkinan hasil pada masing-masing koin. Setiap koin dapat menghasilkan sisi gambar (G) atau angka (A).
- Langkah 2: Susun semua kemungkinan hasil dari pelemparan dua koin. Misalnya, koin pertama sisi gambar (G), koin kedua sisi angka (A), ditulis sebagai (G, A). Kemungkinan lain adalah (G, G), (A, G), dan (A, A).
- Langkah 3: Tuliskan semua kemungkinan hasil tersebut dalam bentuk himpunan. Ruang sampelnya adalah (G, G), (G, A), (A, G), (A, A)
Ilustrasi: Bayangkan dua koin dilempar secara bersamaan. Ada empat kemungkinan hasil yang dapat diamati, yaitu dua sisi gambar, gambar dan angka, angka dan gambar, dan dua sisi angka.
Contoh Soal 2: Pengambilan Bola dari Kotak
Sebuah kotak berisi 3 bola merah (M1, M2, M3) dan 2 bola biru (B1, B2). Jika diambil 2 bola secara acak tanpa pengembalian, tentukan ruang sampelnya.
| Pengambilan Pertama | Pengambilan Kedua | Hasil |
|---|---|---|
| M1 | M2 | (M1, M2) |
| M1 | M3 | (M1, M3) |
| M1 | B1 | (M1, B1) |
| M1 | B2 | (M1, B2) |
| M2 | M1 | (M2, M1) |
| M2 | M3 | (M2, M3) |
| M2 | B1 | (M2, B1) |
| M2 | B2 | (M2, B2) |
| M3 | M1 | (M3, M1) |
| M3 | M2 | (M3, M2) |
| M3 | B1 | (M3, B1) |
| M3 | B2 | (M3, B2) |
| B1 | M1 | (B1, M1) |
| B1 | M2 | (B1, M2) |
| B1 | M3 | (B1, M3) |
| B1 | B2 | (B1, B2) |
| B2 | M1 | (B2, M1) |
| B2 | M2 | (B2, M2) |
| B2 | M3 | (B2, M3) |
| B2 | B1 | (B2, B1) |
Ilustrasi: Kotak berisi bola merah dan biru. Ruang sampel menunjukkan semua kemungkinan kombinasi dua bola yang dapat diambil secara acak tanpa pengembalian. Perhatikan bahwa (M1, M2) dan (M2, M1) adalah hasil yang berbeda karena urutan pengambilannya berbeda.
Penerapan dalam Kehidupan Sehari-hari
Konsep ruang sampel banyak diterapkan dalam berbagai aspek kehidupan sehari-hari, misalnya dalam permainan dadu, lotre, atau bahkan perencanaan perjalanan.
Hubungan dengan Materi Lain
Pemahaman tentang ruang sampel sangat krusial dalam berbagai cabang matematika, terutama dalam peluang dan statistik. Konsep ini membentuk fondasi untuk menghitung kemungkinan terjadinya suatu peristiwa. Kemampuan memahami ruang sampel akan membantu dalam menganalisis data dan menyelesaikan permasalahan yang kompleks di berbagai bidang.
Hubungan dengan Peluang
Ruang sampel merupakan pondasi utama dalam perhitungan peluang. Setiap elemen dalam ruang sampel mewakili kemungkinan hasil dari suatu percobaan. Peluang suatu peristiwa didefinisikan sebagai perbandingan antara banyaknya elemen dalam ruang sampel yang merupakan peristiwa tersebut dengan total banyaknya elemen dalam ruang sampel. Semakin besar jumlah elemen yang memenuhi suatu peristiwa dalam ruang sampel, semakin besar pula peluang terjadinya peristiwa tersebut.
- Contoh: Jika kita melempar sebuah koin, ruang sampelnya adalah kepala, ekor. Peluang munculnya kepala adalah 1/2, karena hanya ada satu hasil ‘kepala’ dari dua kemungkinan dalam ruang sampel.
- Contoh lain: Dalam sebuah kotak terdapat 5 bola merah dan 3 bola biru. Jika diambil satu bola secara acak, ruang sampel terdiri dari 8 bola. Peluang terambil bola merah adalah 5/8.
Hubungan dengan Statistik
Dalam statistik, ruang sampel digunakan untuk mendeskripsikan semua kemungkinan hasil dari suatu pengamatan. Distribusi frekuensi hasil pengamatan dapat divisualisasikan dengan diagram atau grafik, dan pemahaman tentang ruang sampel membantu dalam interpretasi data statistik. Analisis data seringkali bergantung pada identifikasi ruang sampel yang relevan.
- Contoh: Dalam survei pendapat publik, ruang sampelnya adalah semua responden yang berpartisipasi. Hasil survei dapat dianalisis untuk mengidentifikasi tren dan pola dalam ruang sampel tersebut.
- Contoh lain: Dalam eksperimen ilmiah, ruang sampelnya adalah semua kemungkinan hasil dari percobaan tersebut. Data yang dikumpulkan dapat dianalisis untuk melihat apakah hasil tersebut sesuai dengan hipotesis yang diajukan.
Diagram Keterkaitan
Berikut adalah gambaran umum hubungan antara ruang sampel dengan materi terkait:
| Materi | Hubungan dengan Ruang Sampel |
|---|---|
| Peluang | Ruang sampel menjadi dasar untuk menghitung peluang suatu peristiwa. |
| Statistika | Ruang sampel digunakan untuk mendeskripsikan semua kemungkinan hasil pengamatan dan membentuk dasar analisis data. |
Aplikasi di Berbagai Bidang, Materi matematika ruang sampel
Pemahaman tentang ruang sampel dapat diterapkan di berbagai bidang, seperti:
- Ilmu Sosial: Analisis data survei dan riset pasar.
- Ilmu Alam: Eksperimen ilmiah dan analisis data hasil eksperimen.
- Bisnis: Prediksi pasar, analisis risiko investasi, dan manajemen kualitas.
Pemecahan Masalah Kompleks
Pemahaman yang baik tentang ruang sampel sangat membantu dalam menyelesaikan masalah yang kompleks. Dengan mengidentifikasi ruang sampel yang tepat, kita dapat lebih mudah menganalisis kemungkinan hasil dan mengambil keputusan yang lebih baik.
Sebagai contoh, dalam masalah optimasi, pemahaman ruang sampel membantu dalam menentukan kombinasi terbaik yang memenuhi kriteria tertentu.
Cara Mempelajari Materi Ruang Sampel
Memahami ruang sampel dalam matematika membutuhkan pendekatan yang sistematis dan pemahaman konsep dasar. Artikel ini akan memberikan panduan praktis untuk mempelajari materi ruang sampel dengan efektif, mulai dari tips belajar hingga contoh soal dan evaluasi pemahaman.
Tips dan Trik Mempelajari Ruang Sampel
Untuk menguasai materi ruang sampel, penting untuk memahami konsep dasar peluang dan kombinatorika. Latihlah kemampuan menganalisis situasi yang diberikan dan mengidentifikasi kemungkinan-kemungkinan yang terjadi. Berikut beberapa tips:
- Pahami definisi ruang sampel dan kejadian.
- Latihlah dengan berbagai macam contoh, mulai dari yang sederhana hingga yang kompleks.
- Buatlah diagram pohon atau tabel untuk membantu visualisasi ruang sampel.
- Carilah pola atau aturan yang terdapat dalam soal-soal.
- Hubungkan konsep ruang sampel dengan kehidupan sehari-hari, misalnya dalam permainan peluang atau eksperimen.
Langkah-langkah Menyelesaikan Soal Ruang Sampel
Berikut langkah-langkah sistematis untuk menyelesaikan soal ruang sampel:
- Identifikasi ruang sampel dari permasalahan yang diberikan.
- Tentukan semua kemungkinan hasil dari eksperimen atau kejadian yang diamati.
- Buatlah representasi visual, seperti diagram pohon atau tabel, untuk mempermudah identifikasi ruang sampel.
- Jika diperlukan, gunakan prinsip perkalian atau penjumlahan dalam menghitung jumlah anggota ruang sampel.
- Tentukan kejadian yang diinginkan dalam soal.
- Hitung jumlah anggota dari kejadian yang diinginkan.
- Hitung peluang kejadian tersebut dengan membagi jumlah anggota kejadian dengan jumlah anggota ruang sampel.
Ringkasan Materi Penting Ruang Sampel
Materi inti dalam ruang sampel meliputi:
- Ruang Sampel (S): Himpunan semua kemungkinan hasil dari suatu percobaan.
- Kejadian (E): Subhimpunan dari ruang sampel yang memuat hasil-hasil tertentu yang diinginkan.
- Peluang (P(E)): Ukuran kemungkinan suatu kejadian terjadi, dihitung dengan membagi jumlah anggota kejadian dengan jumlah anggota ruang sampel.
- Diagram Venn/Pohon: Alat bantu visual untuk memetakan kemungkinan hasil dalam ruang sampel.
Contoh Soal dan Pembahasan
Berikut contoh soal dan pembahasannya:
| Soal | Pembahasan |
|---|---|
| Dua dadu dilempar bersamaan. Tentukan ruang sampel dan peluang muncul mata dadu berjumlah 7. | Ruang sampel (S) terdiri dari 36 kemungkinan hasil. Kejadian muncul mata dadu berjumlah 7 adalah (1,6), (2,5), (3,4), (4,3), (5,2), (6,1). Peluang kejadian ini adalah 6/36 = 1/6. |
Evaluasi Pemahaman Diri
Untuk mengevaluasi pemahaman, cobalah selesaikan soal-soal berikut:
- Sebuah koin dilempar tiga kali. Tentukan ruang sampel dan peluang muncul paling sedikit dua sisi angka.
- Dua kartu diambil secara acak dari satu set kartu bridge. Tentukan ruang sampel dan peluang terambilnya dua kartu As.
Kemudian bandingkan hasil Anda dengan pembahasan di atas untuk menilai pemahaman Anda terhadap materi ruang sampel.
Latihan Soal dan Jawaban: Materi Matematika Ruang Sampel
Berikut ini disajikan beberapa latihan soal ruang sampel dengan tingkat kesulitan yang berbeda. Setiap soal dilengkapi dengan kunci jawaban dan pembahasan untuk memudahkan pemahaman. Soal-soal ini disusun berdasarkan tingkat kesulitan, mulai dari mudah hingga sedang.
Soal Latihan Tingkat Mudah
Soal-soal berikut dirancang untuk mengasah pemahaman dasar mengenai ruang sampel. Pahami dengan seksama setiap langkah penyelesaian untuk menguatkan konsep.
- Sebuah koin dilempar dua kali. Tentukan ruang sampel dari percobaan tersebut.
- Sebuah dadu dilempar sekali. Tentukan ruang sampel dari percobaan tersebut.
- Sebuah kantong berisi 3 bola merah dan 2 bola biru. Jika diambil satu bola secara acak, tentukan ruang sampel dari percobaan tersebut.
Soal Latihan Tingkat Sedang
Soal-soal berikut menantang pemahaman Anda dalam menentukan ruang sampel dengan sedikit lebih kompleks.
- Dua dadu dilempar bersamaan. Tentukan ruang sampel dari percobaan tersebut, serta hitung berapa banyak elemen dalam ruang sampel.
- Sebuah kotak berisi 5 bola bernomor 1, 2, 3, 4, dan 5. Dua bola diambil secara acak tanpa pengembalian. Tentukan ruang sampel dari percobaan tersebut.
- Sebuah keluarga merencanakan memiliki 3 anak. Tentukan ruang sampel dari kemungkinan jenis kelamin ketiga anak tersebut. Gunakan ‘L’ untuk laki-laki dan ‘P’ untuk perempuan.
Kunci Jawaban dan Pembahasan
Berikut ini kunci jawaban dan pembahasan untuk setiap soal latihan di atas. Perhatikan langkah-langkah penyelesaian yang ditampilkan.
| No Soal | Jawaban | Pembahasan |
|---|---|---|
| 1 | HH, HT, TH, TT | Setiap lemparan koin menghasilkan dua kemungkinan (H atau T). Dengan dua lemparan, terdapat 4 kemungkinan hasil. |
| 2 | 1, 2, 3, 4, 5, 6 | Setiap sisi dadu memiliki angka 1 hingga 6. |
| 3 | Merah, Biru | Hanya ada dua kemungkinan warna bola yang dapat diambil. |
| 4 | (1,1), (1,2), …, (6,6) Terdapat 36 elemen | Setiap dadu memiliki 6 kemungkinan angka. Dengan dua dadu, terdapat 6 x 6 = 36 kemungkinan hasil. |
| 5 | (1,2), (1,3), …, (5,4), (5,3), (5,2), (5,1) | Menggunakan kombinasi, banyaknya kemungkinan pengambilan dua bola adalah 10. |
| 6 | LLL, LLP, LPP, LPP, PLL, PLP, PPL, PPP | Setiap anak memiliki 2 kemungkinan jenis kelamin. Dengan 3 anak, terdapat 2 x 2 x 2 = 8 kemungkinan. |
Ringkasan Terakhir
Kesimpulannya, materi ruang sampel memberikan kerangka kerja yang sistematis untuk menganalisis kemungkinan hasil dari suatu percobaan. Dengan pemahaman yang kuat tentang definisi, jenis-jenis, dan contoh penerapannya, kita dapat dengan lebih mudah memahami dan memecahkan masalah dalam konteks peluang dan statistik. Semoga penjelasan ini dapat membantu dalam proses pembelajaran Anda.